Device Physics
Chp. 1: Review of Quantum Physics
Most of atomic and subatomic physics cannot be explained by classical physics, which is used for macro-objects like stars and planets. Quantum physics was introduced to address gaps in classical physics. Let us go through some fundamentals to understand what led to the birth of quantum physics.
1.1 Photoelectric Effect
Hertz observed the photoelectric effect (i.e., shining light on a material emits electrons) but could not explain why increasing the intensity of light did not result in the emission of electrons with higher energy. In 1905, Einstein proposed that the energy of light is quantized and consists of discrete packets called photons. The energy of each photon is given by:
\[
E = hf
\]
where \( h \) is Planck’s constant, and \( f \) is the frequency of light.
A single electron interacts with a single photon. Increasing the light’s intensity increases the number of photons but does not increase the energy of an individual photon. Thus, higher intensity does not produce higher-energy electrons. Instead, to emit more energetic electrons, the frequency of light must be increased. This also means there is a certain threshold frequency below which electrons cannot be emitted because the photons lack sufficient energy.
The idea of quantized energy was introduced earlier by Max Planck in 1900, who discovered that thermal radiation is emitted in discrete packets of energy called quanta. For example, most objects, including humans, radiate thermal energy in the infrared region (invisible to the naked eye), while hotter objects like the Sun radiate in the visible spectrum, which we can see. Also, this is where the term quantum (singular of quanta) originates. It basically means the smallest discrete unit of any physical quantity (e.g., energy, charge). A photon is a quantum of light.
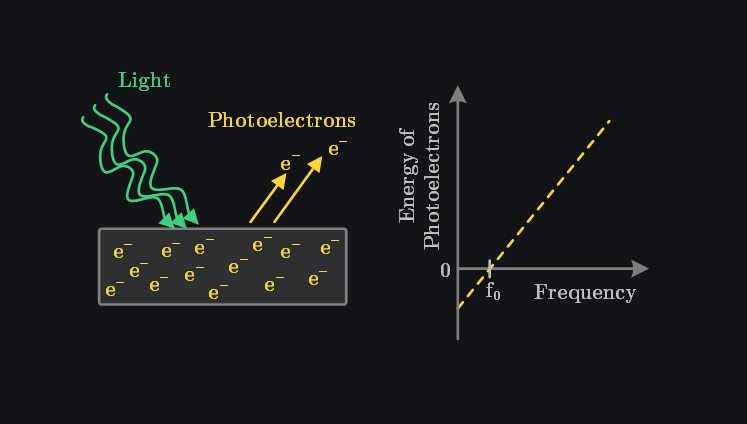
The photoelectric effect was one the experiments that could not be explained by classical theory of light.
1.2 Wave-Particle Duality
In 1924, de Broglie proposed that particles, such as electrons, exhibit wave-like properties too. The wavelength of a matter wave is given by:
\[
\lambda = \frac{h}{p}
\]
where \( \lambda \) is the wavelength, \( p \) is the particle’s momentum, and \( h \) is Planck’s constant.
Q: Why Don’t We See Macro Objects Behaving Like Waves Too?
For large objects like a planet or even a baseball, the mass is enormous compared to tiny particles like electrons. This leads to an extremely small wavelength, often much smaller than the size of an atomic nucleus. Such tiny wavelengths are practically impossible to detect, and any wave-like effects (like interference or diffraction) become negligible. In contrast, electrons have very small masses, resulting in larger wavelengths that are observable in experiments like the double-slit experiment.
1.3 Heisenberg Uncertainty Principle
In 1927, Heisenberg stated that it is impossible to simultaneously determine both the position and momentum of a particle with absolute accuracy. Similarly, one cannot precisely determine both the energy of a particle and the time at which it has that energy.
The uncertainty principle serves as a fundamental safeguard of quantum mechanics. Heisenberg realized that if it were possible to measure both the position and momentum of a particle with perfect accuracy, the entire framework of quantum mechanics would fail. To address this, he proposed that such precise simultaneous measurement must be fundamentally impossible. Scientists then explored various methods to achieve this, but none succeeded in overcoming this fundamental limit [1].
1.4 Birth of Quantum Physics – Schrodinger’s Wave Function
The various experimental results involving light and particles, which could not be explained by classical laws of physics, showed that a revised formulation of mechanics was required. Schrodinger, in 1926, provided a formulation called wave mechanics, which incorporated the principles of quanta introduced by Planck, and the wave–particle duality principle introduced by de Broglie. Schrodinger introduced the concept of the wave function, \( \Psi(x, t) \), which describes the probability of finding a particle at a particular place and time. Max Born postulated that if you take the square of this, it becomes independent of time and what you get is a probability distribution function \(|\Psi(x,t)|^2=|\Psi(x)|^2\) i.e., you can work without notion of time to describe the probability of finding electron at some position x.
We do not need to take a deep dive here. Let’s just introduce Schrodinger equation and move on. In 3D spherical coordinates, the time-independent Schrodinger equation for the hydrogen atom is:
where:
- \( \nabla^2 \): Laplacian operator in spherical coordinates.
- \( \hbar \): Reduced Planck’s constant.
- \( m \): Mass of the electron.
- \( e \): Charge of the electron.
- \( \psi(r, \theta, \phi) \): Wave function.
- \( E \): Energy of the electron.
1.4.1 Quantum Numbers and Quantum States
Solving the 3D Schrodinger equation for an atom yields three numbers (\( n \), \( l \), \( m_l \)) that describe the electron’s energy level (orbit), shape of orbital, and orientation of orbital respectively. A fourth number (\( m_s \)) was added later on to account for the electron’s intrinsic spin. These are collectively known as quantum numbers, and each unique combination of these numbers represents a distinct quantum state of the electron.
1.4.2 Pauli Exclusion Principle
The Pauli Exclusion Principle states that no two electrons in an atom can occupy the same quantum state. If electrons were indistinguishable (that is if they had same quantum state), they would all collapse into the lowest energy state, making the existence of elements and the periodic table impossible. This principle ensures that electrons occupy distinct quantum states, giving rise to the diversity of chemical elements.1.4.3 Radial Distribution of Electrons
While Bohr proposed that electrons orbit the nucleus at fixed distances (shells), quantum physics refines this view by describing a radial probability distribution. This distribution shows the probability of finding an electron at various distances from the nucleus. The highest probability does correspond to the distances predicted by Bohr, but it also shows that electrons are not localized, and they exist as a “cloud” around the nucleus.

1.5 Tunneling in Quantum Physics
1.5.1 Potential Well
In an atom, electrons are confined to a finite space around the nucleus because of the Coulomb attraction between the positively charged nucleus (protons) and negatively charged electrons. This finite space is called a potential well. They cannot move too far from the nucleus due to proton attraction or come too close due to repulsion from other electrons. To intuitively understand a potential well, imagine rolling a ball into a valley. The valley represents the potential well, and just as the ball would naturally stay in the valley due to gravity, electrons remain near the nucleus because of the attractive force between opposite charges. To “escape” the valley, the ball (electron) would need additional energy to climb out, just as an electron would need energy to overcome the Coulomb attraction and escape the atom.
Image below shows an electron in a potential well and its wavefunction (i.e., probability of finding it within potential well)

1.5.2 Tunneling
Electrons in a potential well are confined due to Coulomb forces. However, there is a small probability that an electron can pass through a potential barrier even when it does not have enough energy to classically overcome it. This is called tunneling. Solving the Schrodinger equation for a potential barrier shows that the wave function does not abruptly end at the barrier (unless the barrier is infinite). Instead, it extends into the barrier and decays exponentially. The extent of penetration depends on the barrier’s height, width, and the electron’s energy.
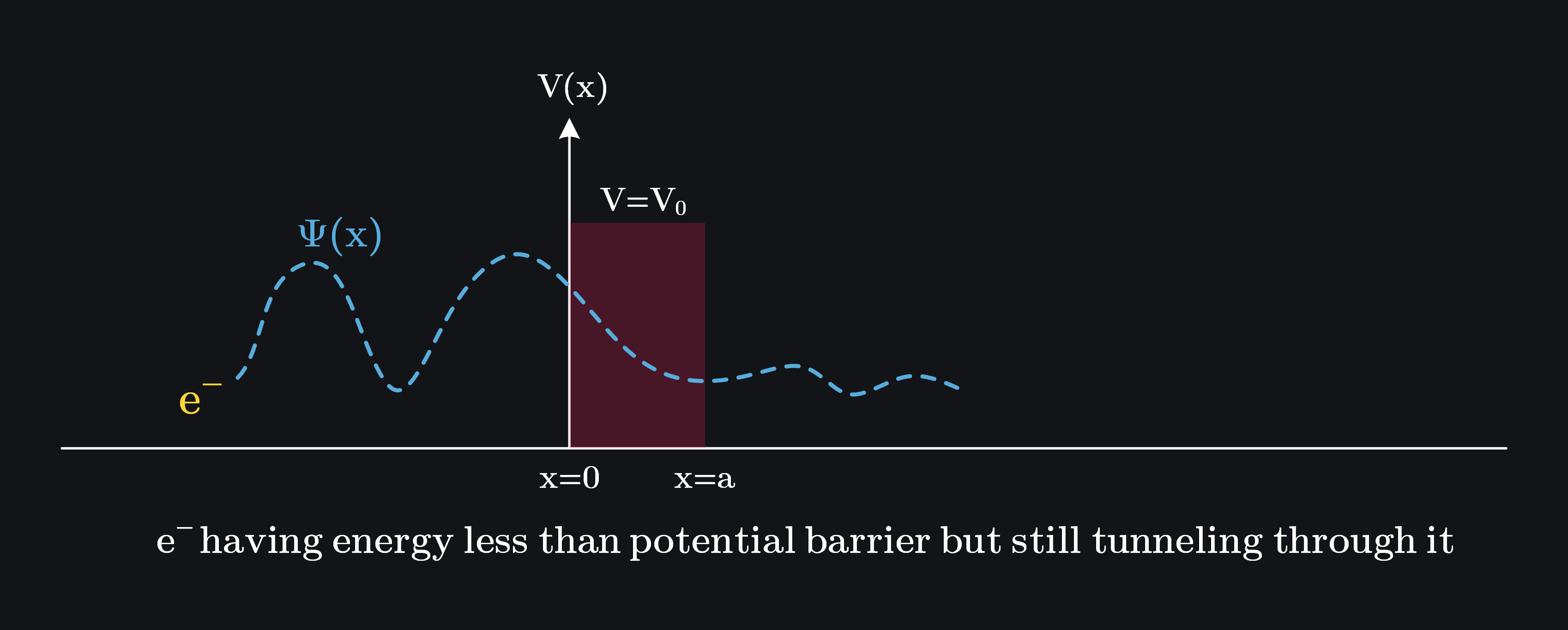
Q: How Can Electrons Tunnel Through a Potential Barrier Higher Than Their Energy?
It can be proven mathematically, but there is not much “analog” insight here how it happens. Heisenberg uncertainty principle saves the day: since we cannot say what was the exact energy of electron at given time, this uncertainty allows for brief fluctuations in energy, enabling the electron to momentarily have enough energy to “pass through” the barrier
Having refreshed some fundamentals, let us now proceed to how energy bands are formed inside semiconductors.
References
[1] The Feynman Lectures on Physics Vol. III Ch. 1: Quantum Behavior
[2] “Semiconductor Physics And Devices: Basic Principles” by Donald A. Neamen
Browse by Tags
RFInsights
Published: 07 Feb 2025
Last Edit: 07 Feb 2025