TX IQ Mixer
We want to upconvert our baseband signal, \(\omega_{bb}\) , to an RF frequency, \(\omega_{lo}+\omega_{bb}\). The easiest and probably the only way alive of doing so is to multiply \(\omega_{bb}\) signal with \(\omega_{lo}\) signal. This works and generates two sidebands, \(\omega_{lo}+\omega_{bb}\) & \(\omega_{lo}-\omega_{bb}\). But in almost all of the applications today, you just want to transmit a single sideband, either \(\omega_{lo}+\omega_{bb}\) called as upper sideband or \(\omega_{lo}-\omega_{bb}\) called as lower sideband. How do we do that? IQ mixers. They let you cancel out an undesired sideband and many baseband emissions. Image below shows a typical TX with IQ Mixer.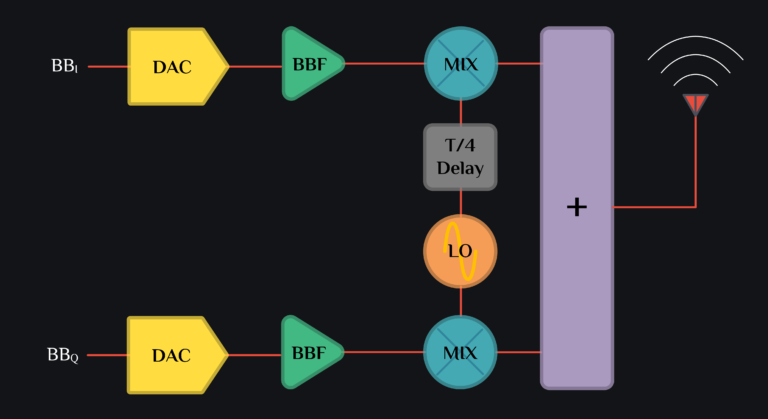
TX IQ Mixer – Math & Insights
Consider an IQ transmitter. I channel DAC generates cosine signal, and Q channel DAC generates 0.25\(T_{bb}\) shifted signal of I channel (or in other words 90 degree shifted for fundamental):
where \(A_{1}\) is a linear gain coefficient, \(A_{3}\) is 3rd order distortion coefficient and \(A_{5}\) is 5th order distortion coefficient. Read more on this in single tone distortion.
I channel baseband signal is multiplied by I channel LO, and Q with Q. We can write mixer output as:
I Channel Mixer Output
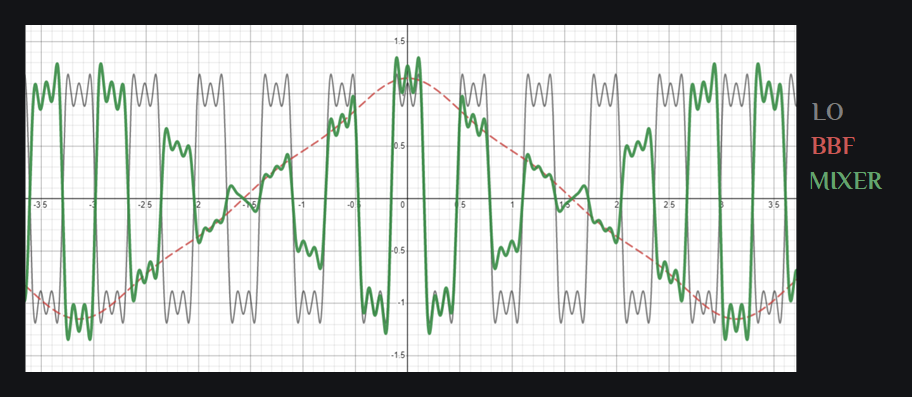
A single mixer generates double sideband signal, that is why your output signal (as shown in green color in image above) looks so messed up. It is sum of two sinusoid (along with many other distortion products). Go ahead and add two sinusoids, you will see it will start looking like green signal above. And don’t mind the ringing on the signal, that is because we only considered up to 5 harmonics of LO (add more in your analysis, and it will start going away). Here is how your output spectrum of a single channel mixer will look like:
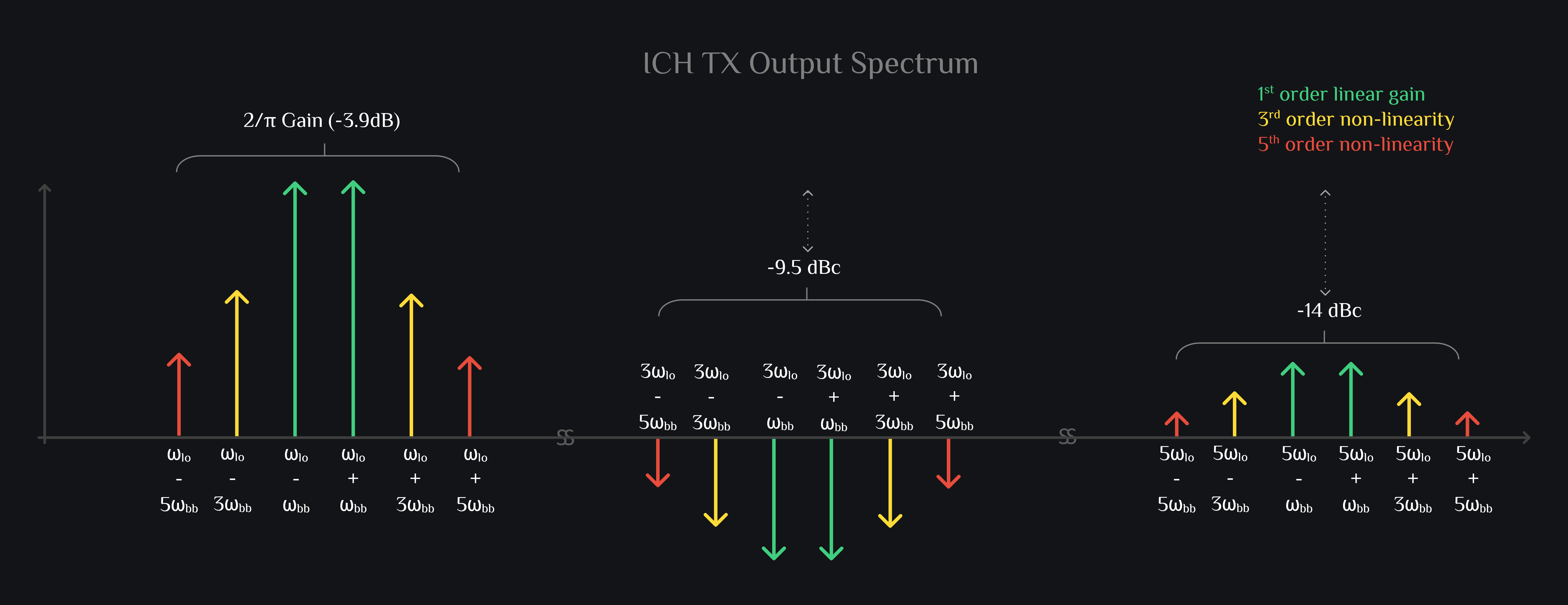
Q Channel Mixer Output
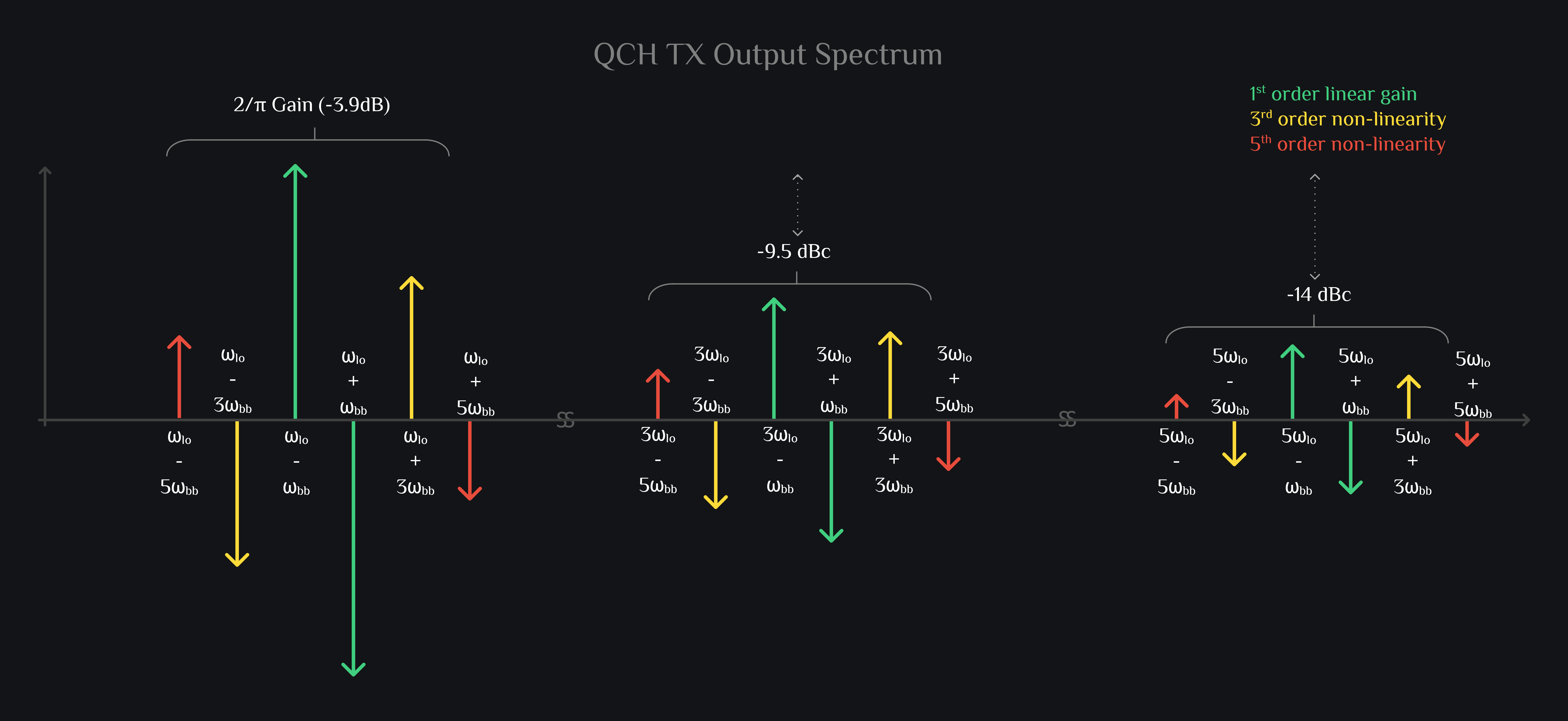
I & Q Mixer Output Combined
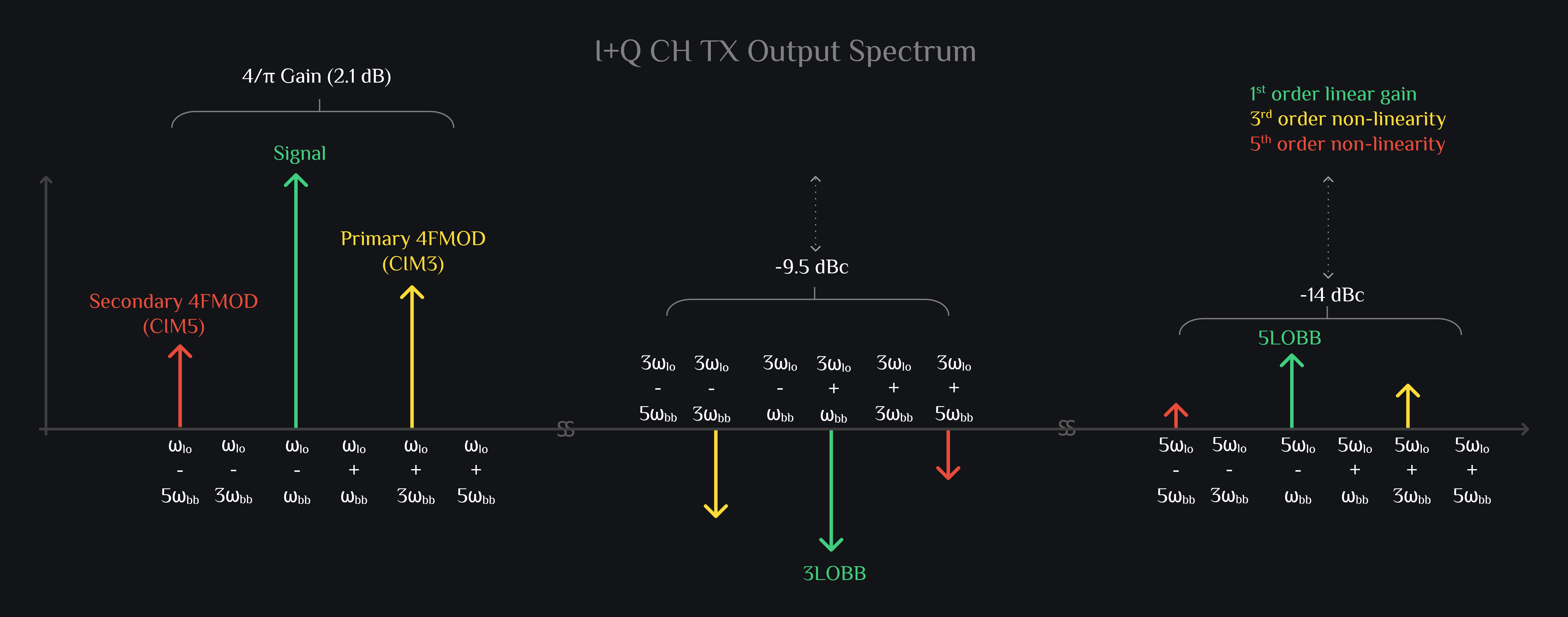
Now this is where it gets interesting. When I and Q channel outputs are added, a lot of products cancel out. These tones are left out:
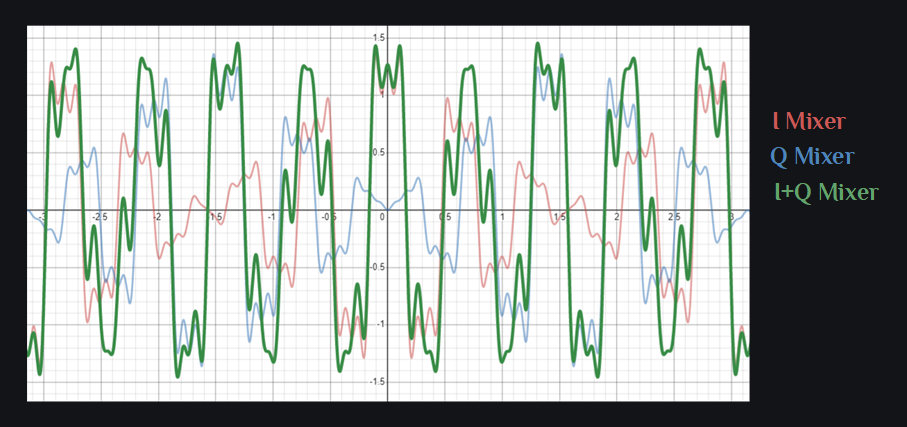
Sad. Even when you canceled a sideband, your signal (as shown in green color in image above) still does not look like a sinusoid. Now you can blame distortion products and the fact that each odd harmonic of LO has a copy of your signal+distortions around it. But hey, we cleaned up spectrum a lot, improved gain of our desired sideband, and rejected undesired sideband. And don’t worry, we have more tricks up our sleeves to clean it up further. Intrigued? You are ready to read HRM Mixer.
Author: RFInsights
Date Published: 15 Jan 2023
Last Edit: 02 Feb 2023