Integrated Transformer Models

We decided to write this article because there are only so many different models of a transformer that exist. Analog IC designers, RFIC designers and mm-wave IC designers – they all understand transformers a little differently. Enough is enough. We are putting together a list of different models (with derivations of course) for your quick reference, and we also show you THE one favored by the most folks.

Integrated Transformer Model # 1 – Base Model

Consider a transformer as shown in image below.

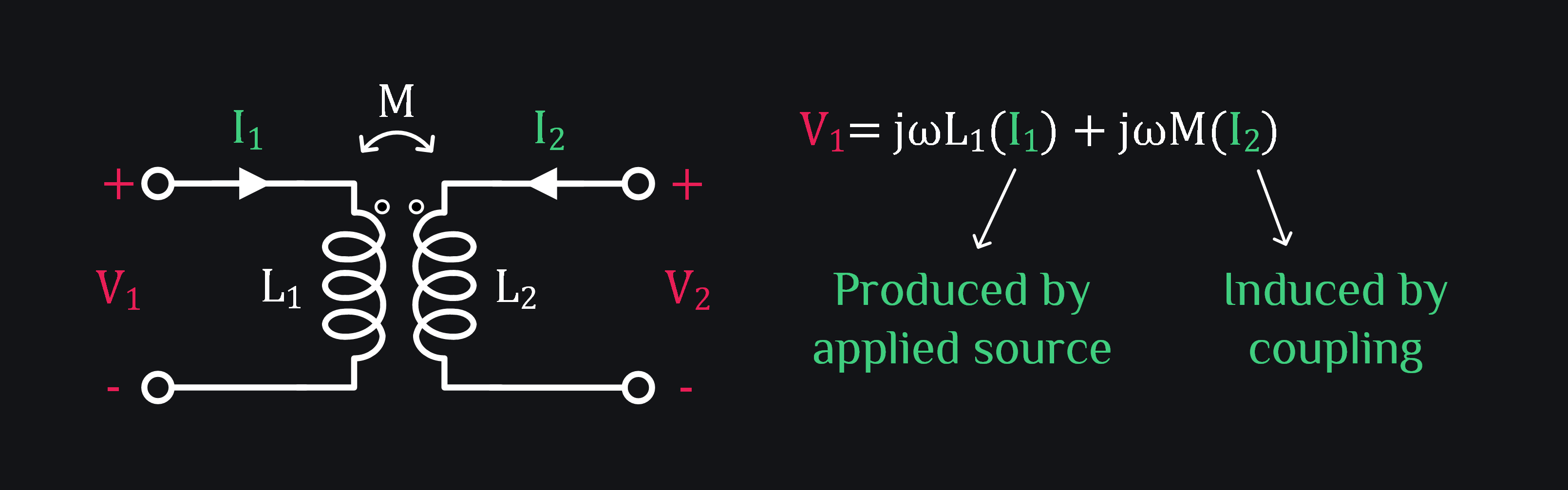
Applied source V₁ consists of two voltage drops: First, the voltage drop produced by the current I₁ which is generated from the V₁ itself. And second, the voltage drop produced by induced current I₂ which is actually generated by V₂. Therefore, we can write V₁ and V₂as:

\begin{alignat*}{3} \\ V_1 &= j\omega L_1(I_1) +j\omega M(I_2)\\ V_2 &= j\omega M(I_1)+j\omega L_2(I_2) \\ \end{alignat*}

\[ \begin{bmatrix} V_1\\ V_2 \end{bmatrix} = \begin{bmatrix} j\omega L_1 \;\;j\omega M\\ j\omega M \;\;j\omega L_2 \end{bmatrix} \begin{bmatrix} I_1\\ I_2 \end{bmatrix} \;\;\;\;(1) \]

Recall that this looks much like a 2-port Z-parameter matrix given as:

\[ \begin{bmatrix} V_1\\ V_2 \end{bmatrix} = \begin{bmatrix} Z_{11} \;\;Z_{12}\\ Z_{21} \;\;Z_{22} \end{bmatrix} \begin{bmatrix} I_1\\ I_2 \end{bmatrix} \]

Therefore, we can say:

$$Z_{11}=j\omega L_1 \;\;\&\;\;Z_{22}=j\omega L_2\;\;\&\;\;Z_{12}=Z_{21}=j\omega M$$

The equivalent circuit for Z-parameters of a reciprocal 2-port network can be given as:

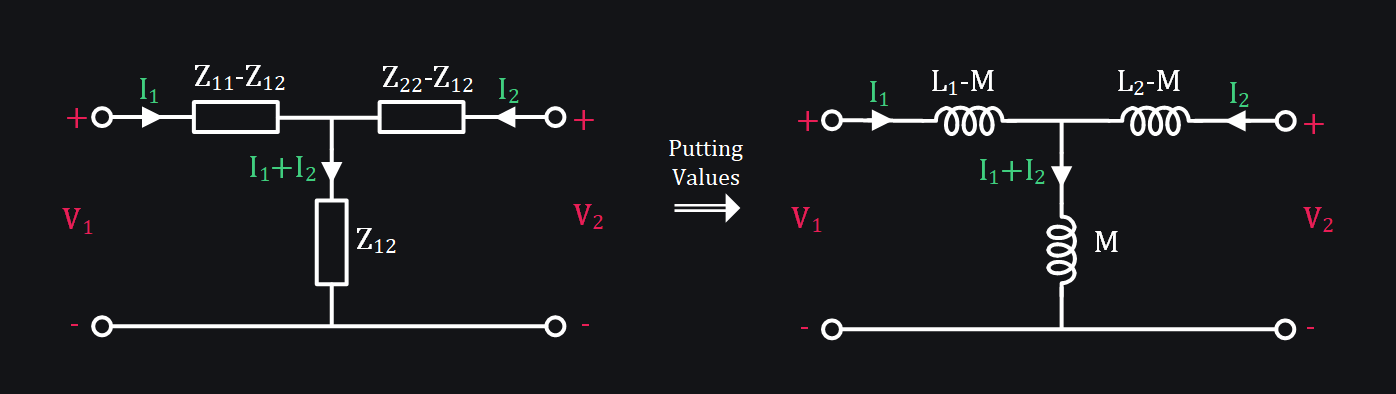
This is the base model of a transformer. It says, if I₂ were zero (i.e., secondary is open-circuited), then applying V₁ and measuring I₁ will only reveal L₁ (which makes sense as primary inductance is L₁). However, the moment you apply some V₂, mutual inductance M will lead to slightly different I₁, thus V₁/I₁ will no longer give you L₁ impedance. It will be different. What shall it be? Let’s improve this base model to answer such questions. Before that, let’s get done with some FAQs.

FAQs

Q: What is difference between M and k?

A: M is real deal. M is real physical thing. M is mutual inductance which is a way of saying how much “extra” voltage is produced in one coil due to magnetic field “coupling” created by I₂ in second coil. k is just a way of saying coupling is not perfect.

Q: Define M

A: $M=\sqrt{L_1L_2}$

Q: Define k

A: k is saying hey this M is going to be less than its value because coupling ain’t good so you’d better write M as $M=k\sqrt{L_1L_2}$ where $0 \le k \le1 $

Q: Base transformer model shown above didn’t talk about turn ratio. How to think of turn ratio?

A: Consider an ideal transformer with turn ratio (N₂/N₁) as n

\begin{equation} \frac{V_2}{I_2} = \frac{nV_1}{\frac{I_1}{n}} = n^2\frac{V_1}{I_1} \;\;\;\;(2) \end{equation} $$ But\;\; \frac{V_2}{I_2} = j\omega L_2\;\;\&\;\; \frac{V_1}{I_1}=j\omega L_1$$ $$\therefore j\omega L_2 = n^2 . j\omega L_1 \implies n = \sqrt{\frac{L_2}{L_1}}$$

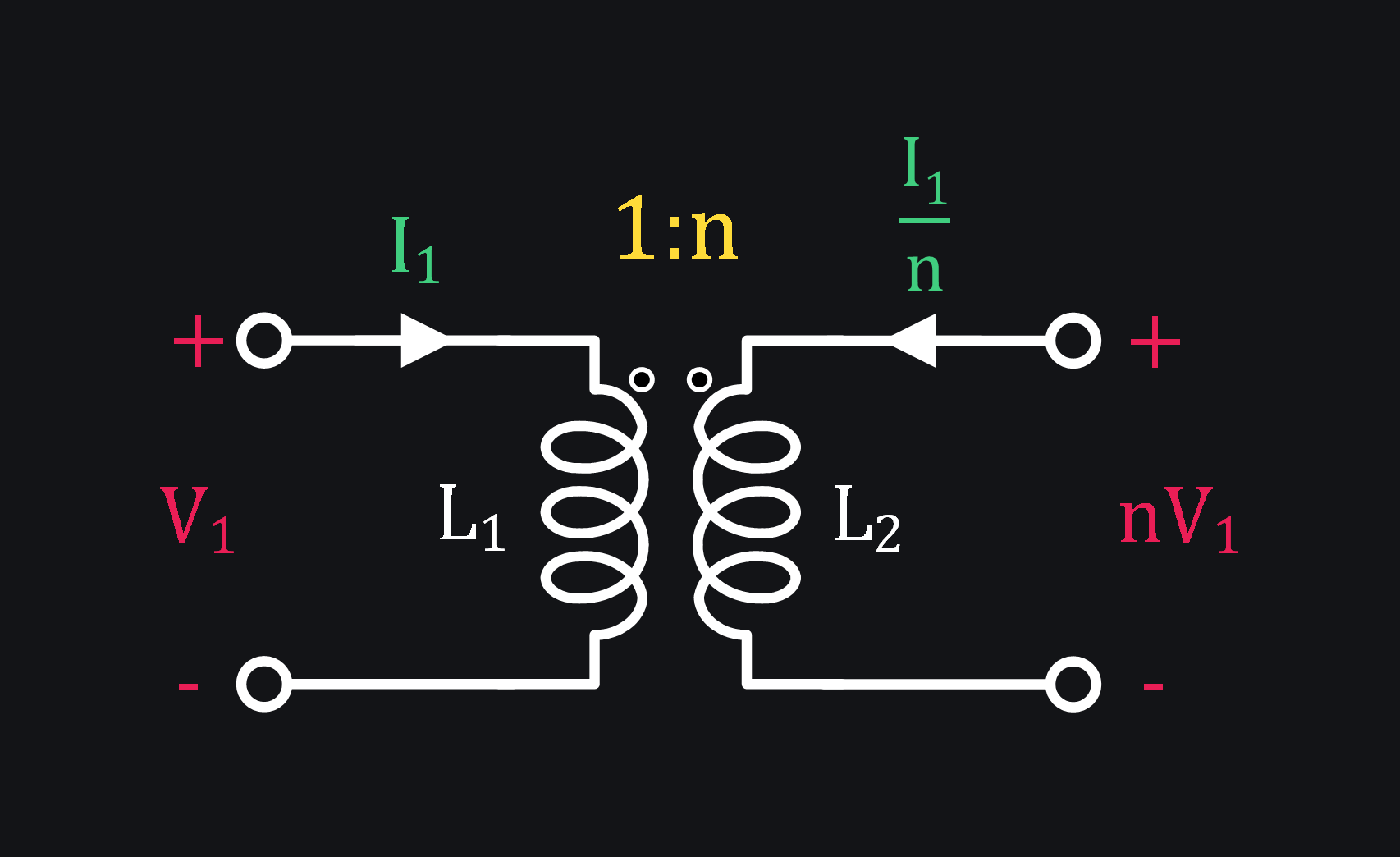
Practical transformer: Hey coupling ain’t perfect, so terminal relations of Eq. (2) won’t hold. Add k.

$$\therefore nk = \sqrt{\frac{L_2}{L_1}} \;\;\; \text{just saying effective number of turns are reduced by factor k}$$ $$\implies n = \frac{1}{k} \sqrt{\frac{L_2}{L_1}}$$

This says you can artificially create turn ratio by choosing k, L₁ and L₂. You don’t have to physically make 2 turns say to create turn ratio of 2!

Integrated Transformer Model # 2 – add Turn Ratio

People would like to separate out turn ratio and keep it as a clear visible metric to quickly transform impedance. So you won’t see the base model being used anywhere at least in IC design.

What do people want? A model like this:

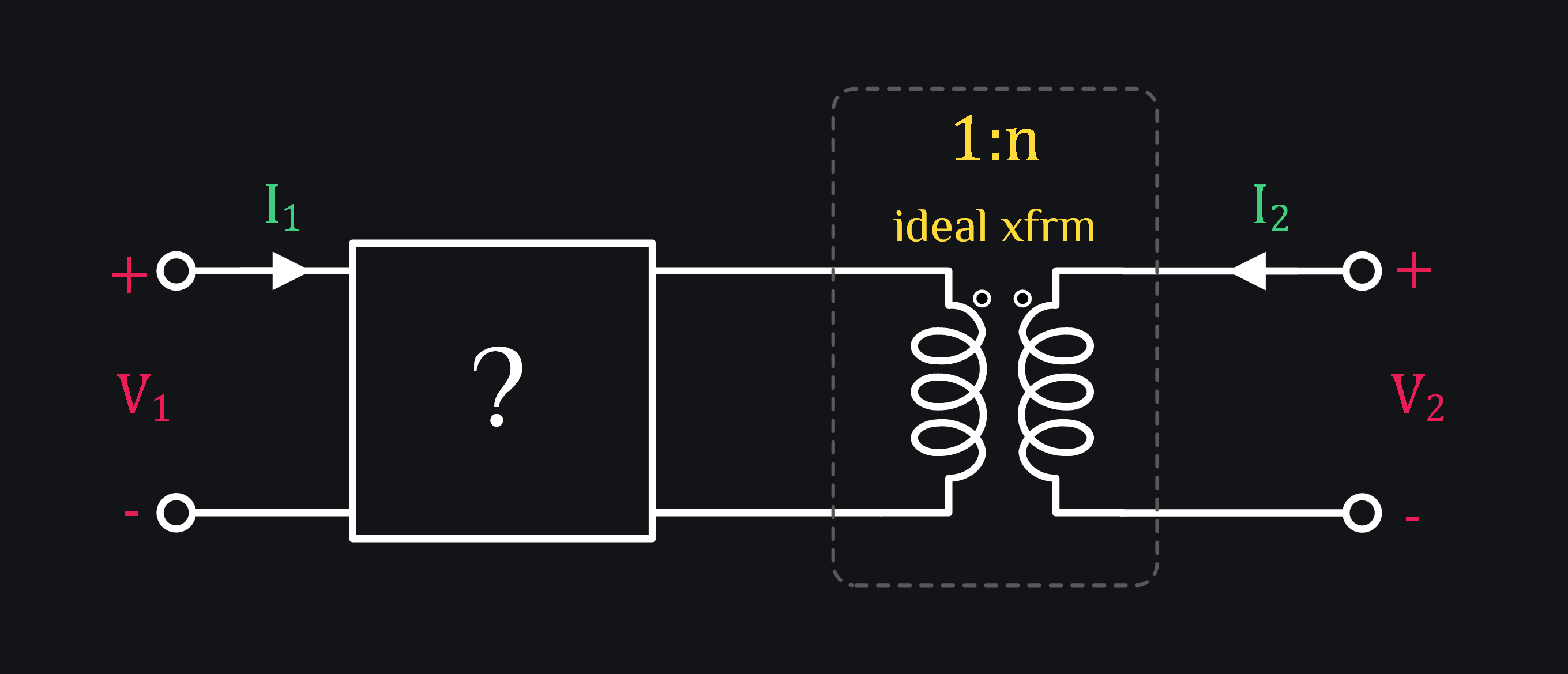
Think about the terminal relations of the black box ? now. They are:

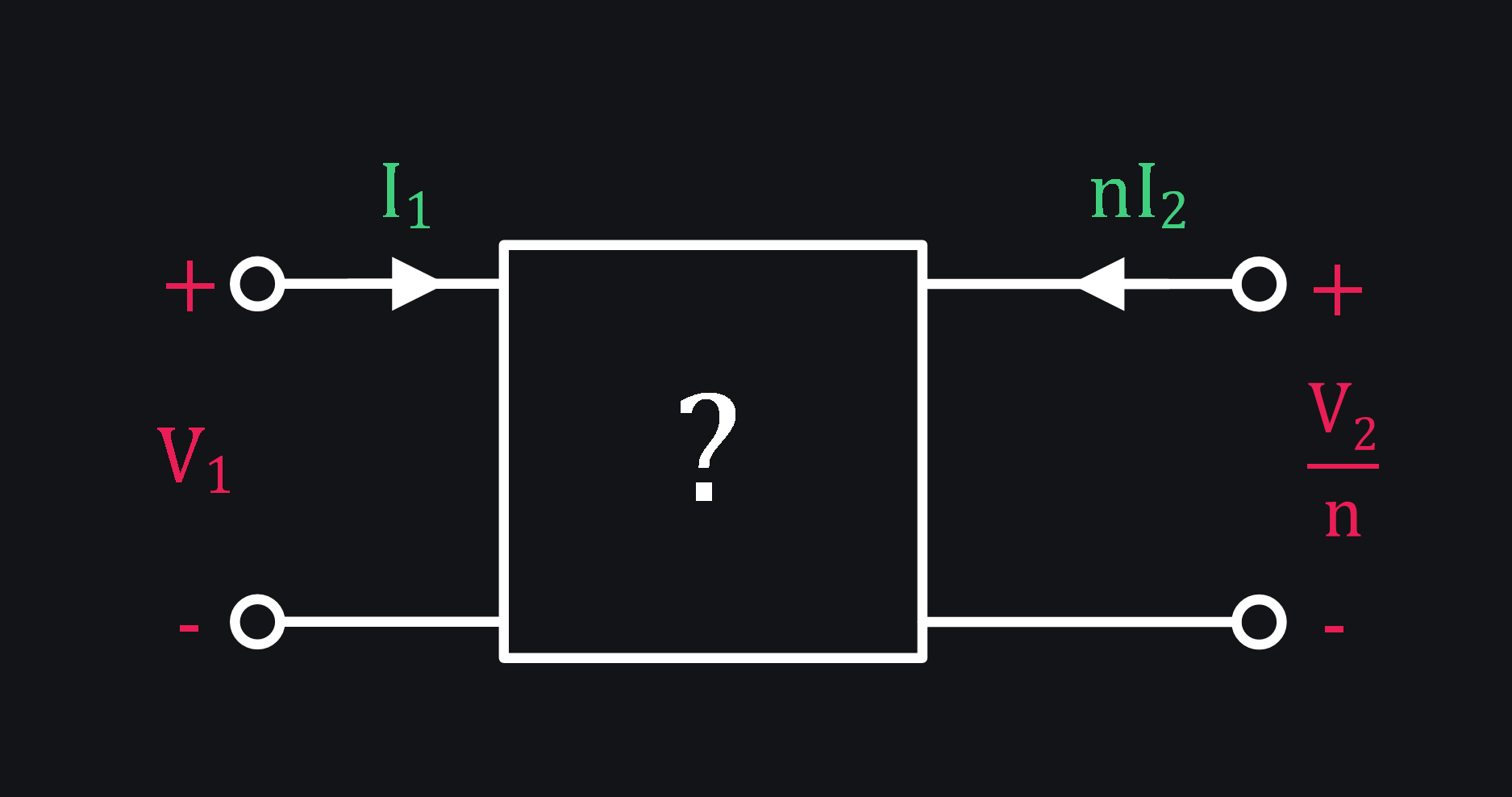
We want to know what kind of transformer can we put here which in series with ideal transformer of 1:n would produce same results as original transformer. Start with writing the z-matrix:

\[ \begin{bmatrix} V_1\\ \frac{V_2}{n} \end{bmatrix} = \begin{bmatrix} j\omega L_1^\prime \;\;j\omega M^\prime\\ j\omega M^\prime \;\;j\omega L_2^\prime \end{bmatrix} \begin{bmatrix} I_1\\ nI_2 \end{bmatrix} \] \[ \begin{bmatrix} V_1\\ V_2 \end{bmatrix} = \begin{bmatrix} j\omega L_1^\prime \;\;nj\omega M^\prime\\ nj\omega M^\prime \;\;n^2j\omega L_2^\prime \end{bmatrix} \begin{bmatrix} I_1\\ I_2 \end{bmatrix} \]

Comparing it with Eq. 1 gives us:

$$L_1^\prime = L_1 \;\;\&\;\; M^\prime = \frac{M}{n} \;\;\&\;\; L_2^\prime = \frac{L_2}{n^2}$$

This says our black box is actually a transformer like this:

Replace this transformer with its base model, and we arrive at the second model of a transformer where you have clearly separated out the turn ratio:

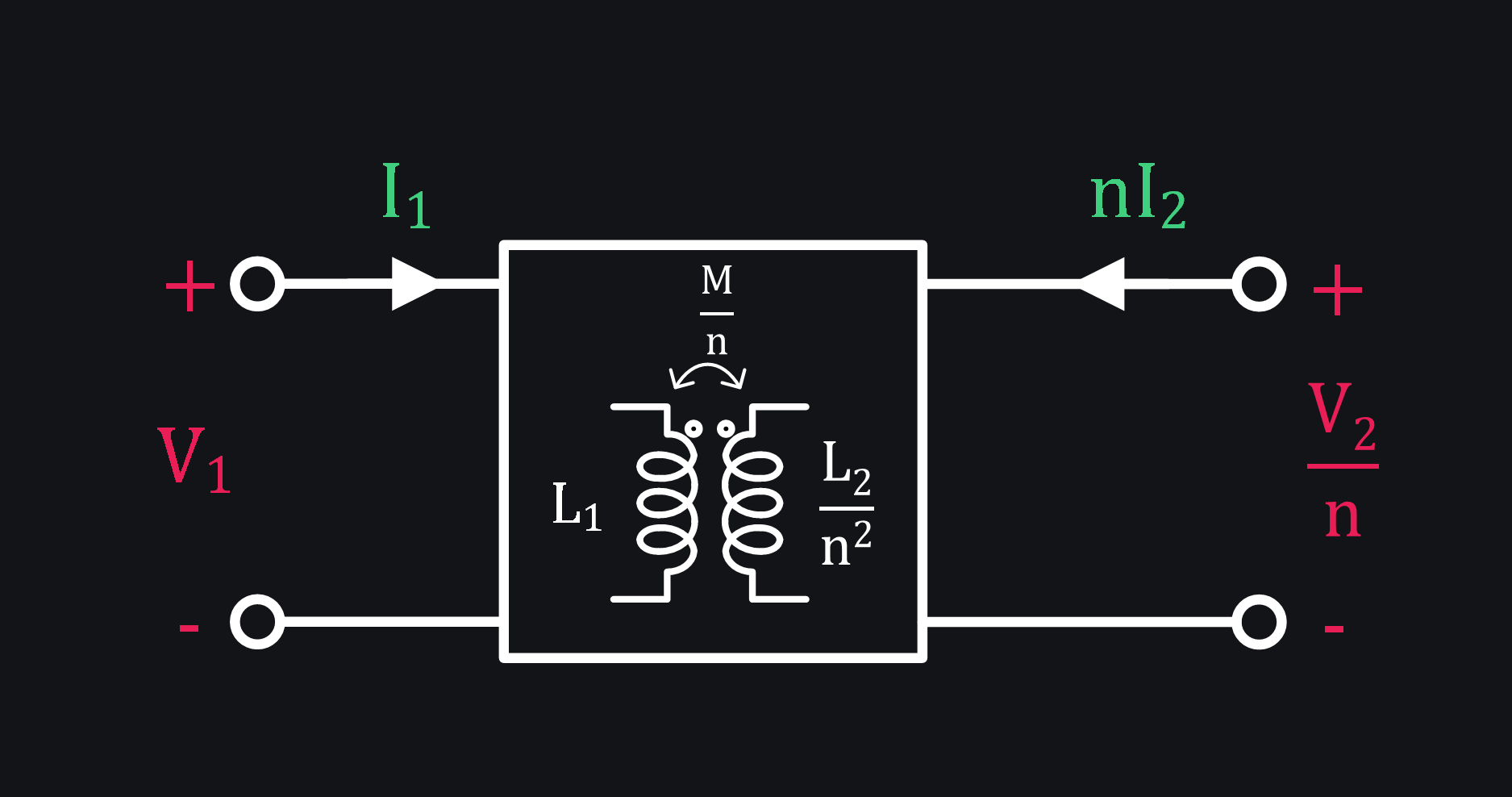
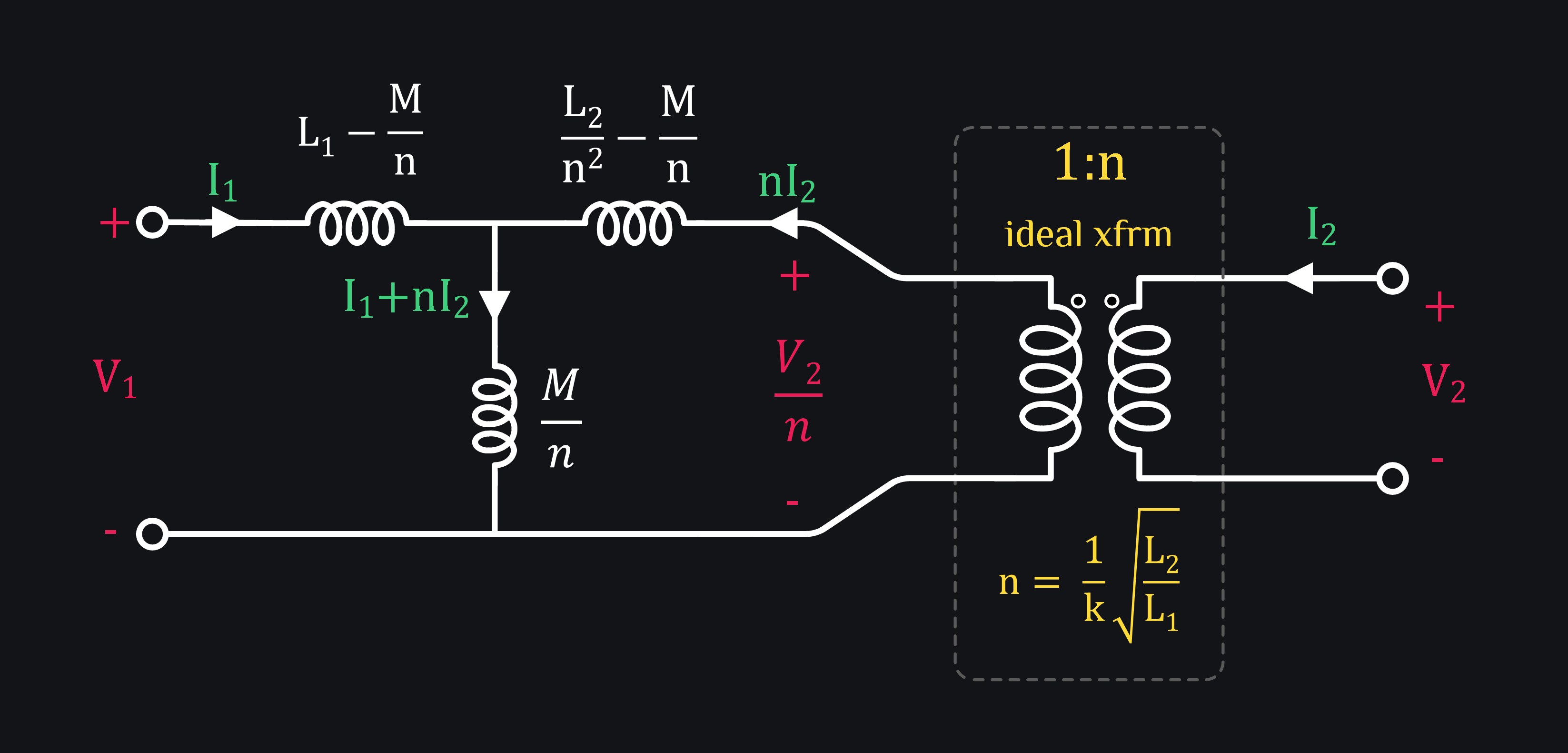
Integrated Transformer Model # 3 – We don’t like M

Engineers just wouldn’t like to see M. They work with k. So let’s get rid of M, ready when you are.

$$\text{Consider} \;\;\; \frac{M}{n} = \frac{k\sqrt{L_1L_2}}{\frac{1}{k}\sqrt{\frac{L_2}{L_1}}} \;\;\;\; \because\left(M=k\sqrt{L_1L_2} \;\;\&\;\; n = \frac{1}{k}\sqrt{\frac{L_2}{L_1}}\right)$$ $$\implies \frac{M}{n} = k^2L_1 \;\;\;\; (3)$$ $$\text{Also consider} \;\;\; \frac{L_2}{n^2}-\frac{M}{n} = \frac{L_2}{\frac{1}{k^2}\frac{L_2}{L_1}}-k^2L_1 = 0 $$

Put these in model # 2, and we arrive at the third model of transformer which happens to be people’s favorite and we recommend you to start with this one.

This model is more intuitive for engineers because it talks to us in our lingo:

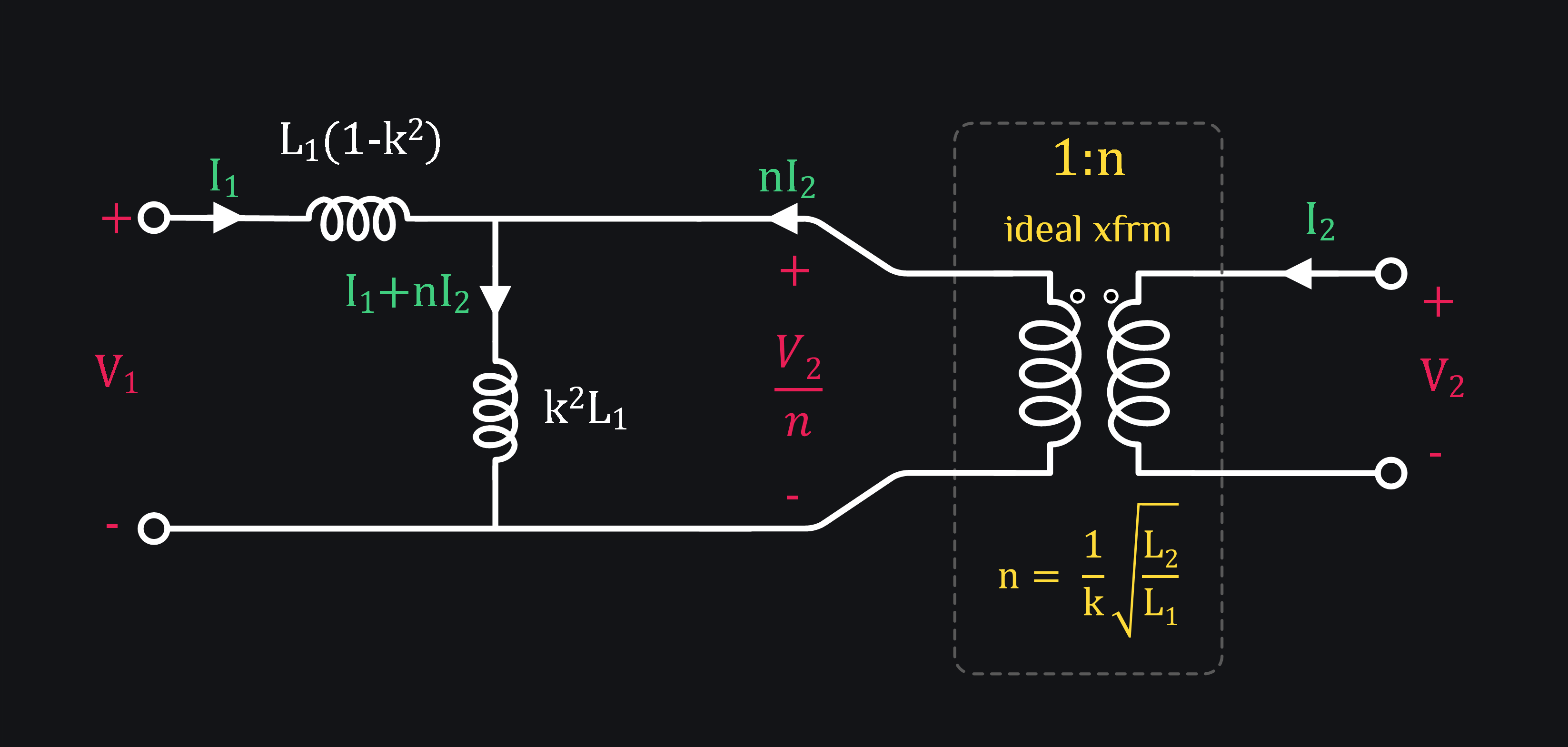
L₁(1-k²) represents drop across “leakage inductance”. It says all of your V₁won’t reach transformer primary because k wasn’t perfect.
k²L₁ represents magnetization inductance because voltage that reached to it is actually what create magnetic fields.

Interesting insights we must say, hey we are not bragging, we are just happy to refresh these insights ourselves.

Integrated Transformer Model # 4 – Where’s my L₂

Some folks are destined to lose it the first time they see above model of transformer. They go like “but where is the secondary inductor (L₂) of transformer, it seems L₁ is all mighty, does that mean L₂ not matter at all? because it’s definitely not in the model”. While it’s not visible, it’s hidden in k and n. Therefore, some folks would use the model shown below (fourth model) where they can clearly see their beloved L₂.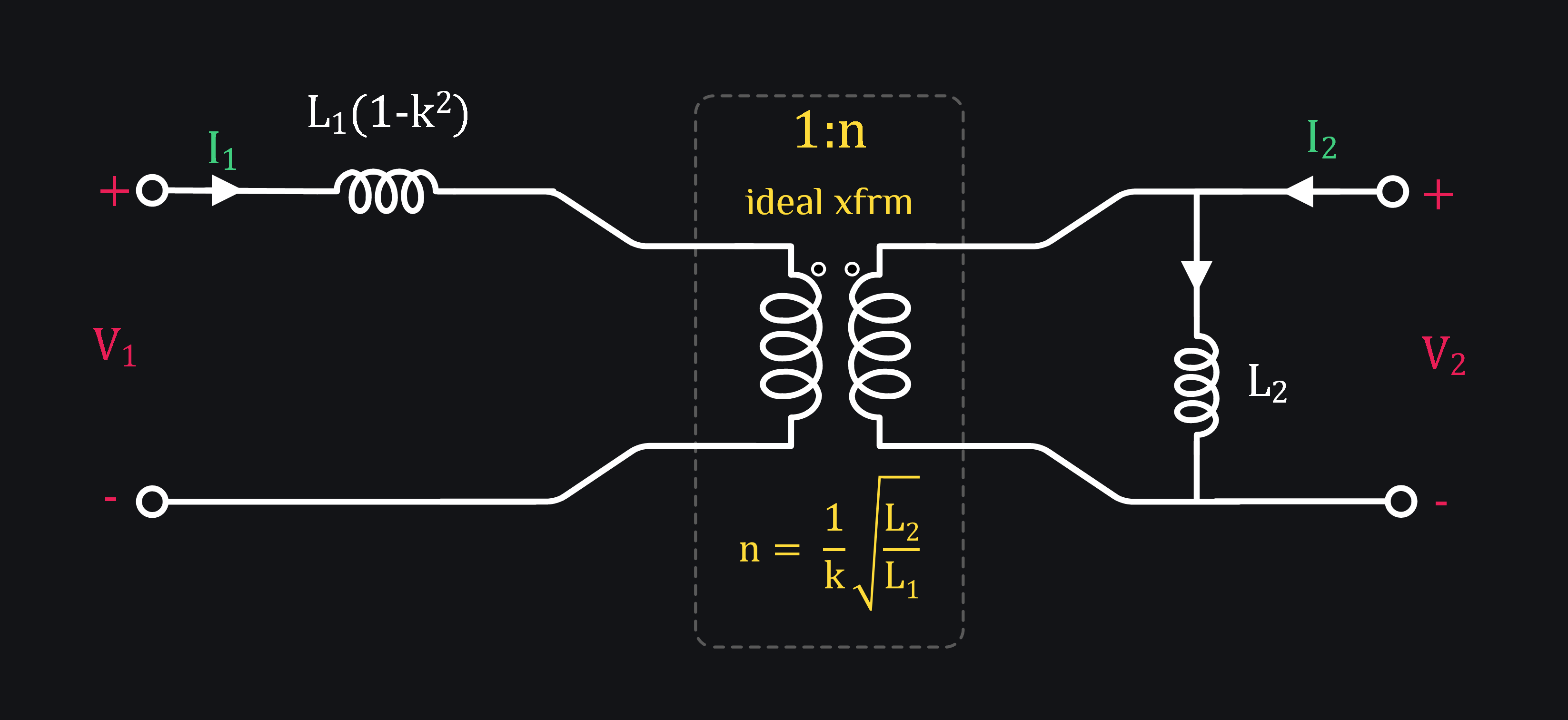

It’s not hard to prove that k²L₁ on primary side becomes L₂ when moved to secondary. Just multiply k²L₁ by n² (because remember an ideal transformer transforms impedance by n²)

$$ k^2L_1 . n^2 = k^2L_1.\frac{1}{k^2}\frac{L_2}{L_1}=L_2$$

Integrated Transformer Model # 5 – Just to Cover the Ground

There is yet another genre of folks who just don’t like to see k in their turn ratio n. It is more intuitive for them to think: “hmm that’s how I need to size my L₁ and L₂ to get this turn ratio n”, whatever k does, it does. We will model it separately. Oh well. Okay. So let’s try to take k out of n and see how our model looks like.

$$\text{Say} \;\;\; n^\prime = nk \;\; \implies n^\prime = \sqrt{\frac{L_2}{L_1}} \;\;\; \left(\because n = \frac{1}{k}\sqrt{\frac{L_2}{L_1}} \right)$$

We know from Eq. (3) that

$$\frac{M}{n} = k^2L_1 = k\frac{M}{n^\prime}$$ $$\therefore \frac{M}{n^\prime} = kL_1$$ $$\implies L_1 - \frac{M}{n^\prime} = L_1(1-k)$$ $$\text{Similarly} \;\;\; \frac{L_2}{n^{\prime 2}}-\frac{M}{n^\prime} = \frac{L_2}{\frac{L_2}{L_1}} - kL_1 = L_1(1-k)$$

Inserting these in second model, we arrive at the fifth model of transformer which is not seen in RFIC design but it does has some symmetry though.

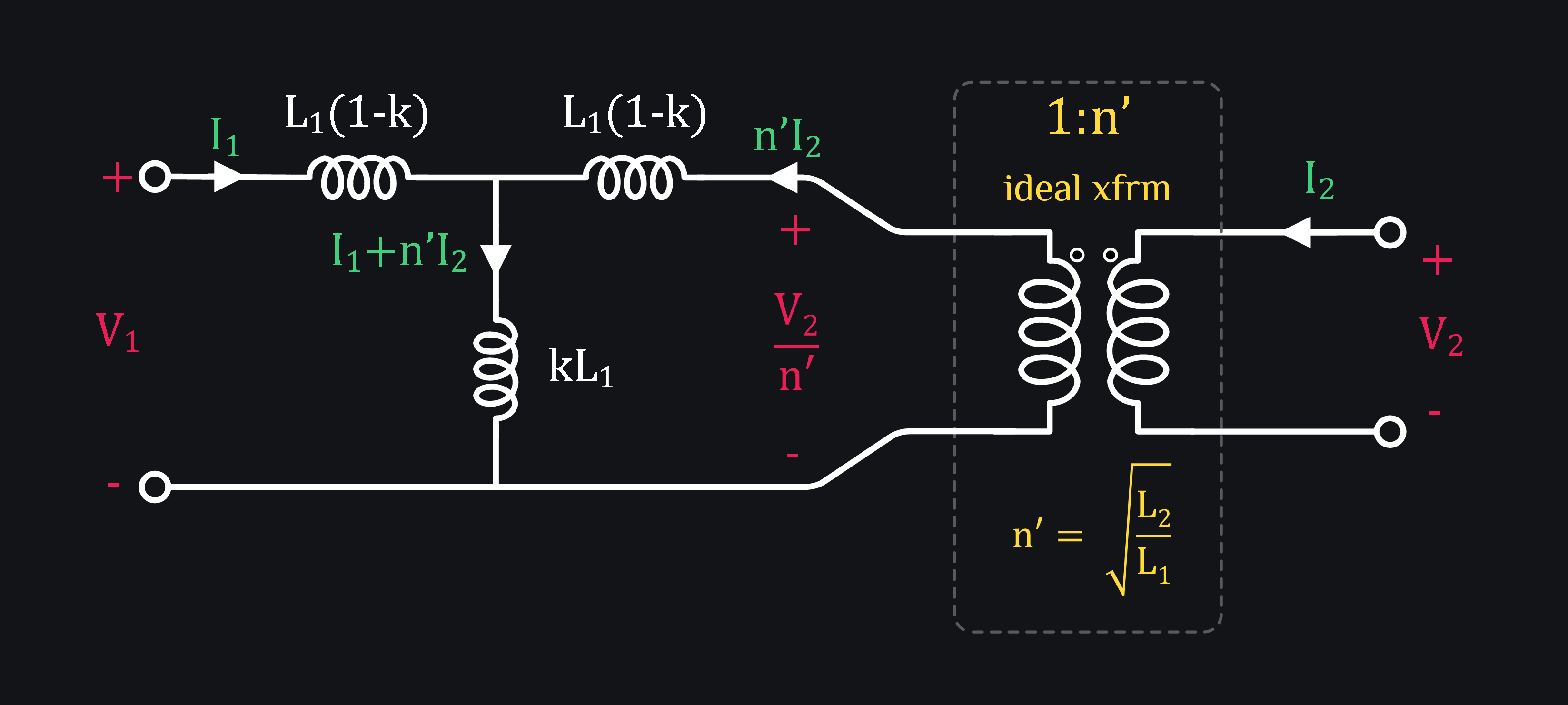
We covered all the transformer models we have encountered so far. Out of all these, we recommend to start with model # 3, and keep others in mind just to build intuition. It all depends on ease of you. Maybe some other model is easier to use for your situation.

Here’s a quick summary of why $ M = \sqrt{L_1L_2} $ for nerdy you.

RFInsights 
Date Published: 01 Jan 2023
Last Edit: 28 Jun 2023