Device Physics

Chp. 3: Intrinsic Carrier Concentration

We eventually wish to describe the current–voltage characteristics of semiconductor devices. Since current is due to the flow of charge, an important step in this process is determining the number of electrons and holes in the semiconductor that will be available for conduction. The number of carriers that can contribute to the conduction process is a function of the number of available quantum states and how many of them are occupied. Let’s explore the concepts of ‘density of states’ and ‘Fermi-Dirac probability’ to calculate the concentration of electrons and holes involved in conduction in semiconductors.

3.1 Density of States

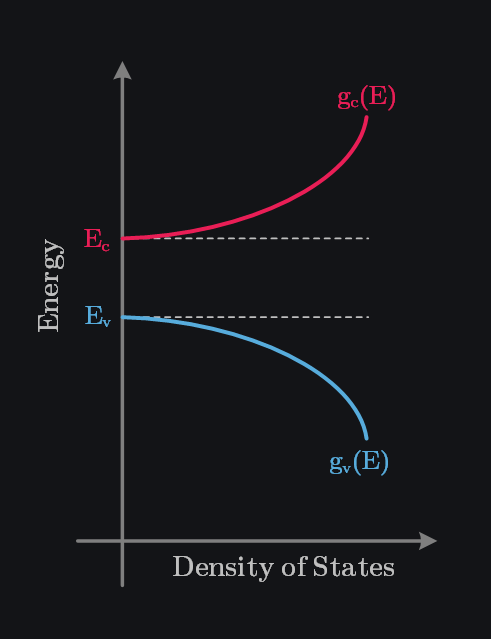
When we discussed the splitting of energy levels into bands of allowed and forbidden energies, we indicated that the band of allowed energies was actually made up of discrete energy levels. The number of these energy levels is called as density of states and can be given as:

g_c(E) = \frac{1}{2\pi^2} \left( \frac{2 m_e^*}{\hbar^2} \right)^{\frac{3}{2}} \sqrt{E - E_c} \] \[ g_v(E) = \frac{1}{2\pi^2} \left( \frac{2 m_h^*}{\hbar^2} \right)^{\frac{3}{2}} \sqrt{E_v - E}

where,

\(E\) is the energy of the electron,
\(E_c\) is the conduction band edge energy,
\(\hbar\) is the reduced Planck’s constant,
\(g_c(E) \text{ & } g_v(E)\) is the density of states in the conduction band and valence bands respectively,
\(m_e^* \text{ & } m_h^*\) is the effective mass of electrons and holes respectively.

If you’re curious, effective mass describes how a particle moves in a crystal under an external force, accounting for the influence of the various potentials arising from the crystal lattice on its motion. When a particle is traveling in free space, its effective mass equals its actual mass, and classical mechanics can be applied.

Q: Why Does Density of States Increase with Increase in Energy of Electrons?

We have already established that higher energy means electrons are farther from the nucleus which means they have more spatial freedom and less attraction to the nucleus (resulting in more complex motion). This leads to more and more distinct quantum states electrons can have. On the other hand, hole density of states decreases with increase in energy. This is because holes are created by the absence of outermost electrons, which are in the valence band. As you move down in energy, you are moving toward inner electrons, which are fewer in number and more tightly bound, thus lower density of states.

3.2 Fermi-Dirac Probability

The probability that a quantum state at the energy \(E\) will be occupied by an electron is given by Fermi-Dirac distribution:

f(E) = \frac{N(E)}{g(E)} = \frac{1}{e^{\dfrac{E - E_F}{kT}} + 1}

where,

\(f(E)\) is Fermi-Dirac probability
\(N(E)\) is number of occupied states
\(g(E)\) is total number of states
\(E_F\) is the Fermi energy

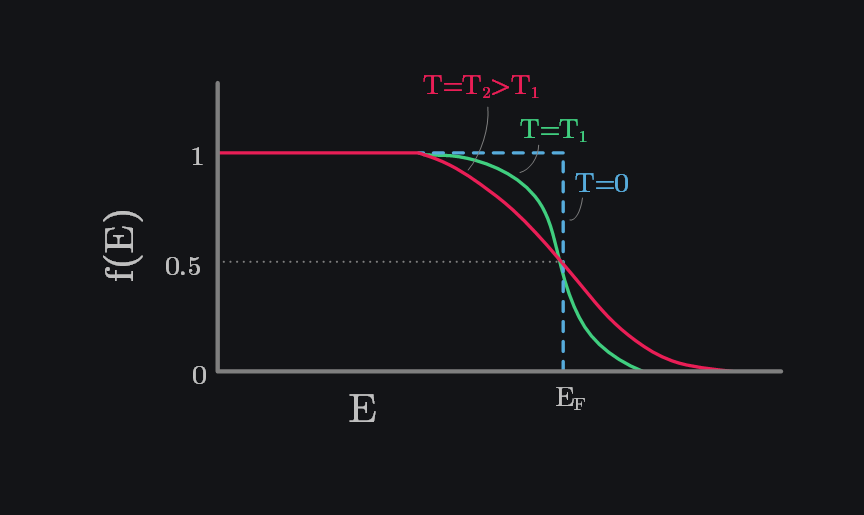
Fermi energy is not an actual allowed energy level. It is a mathematical construct. It is an energy where chance of occupation of quantum state by electron is 50%. Let’s say \(E=E_F\) and \(T>0\), we can see:

f(E) = \frac{1}{e^0 + 1} = 0.5

The image below shows how \(f(E)\) varies with energy \(E\). At \(T=0K\), electrons occupy the lowest possible energy states, and no electron-hole pairs are thermally generated. This means all states in the valence band are completely filled, while the conduction band is entirely empty. In other words, all states below the Fermi energy \(E_F\) are filled (\(f(E)=1 \text{ for } E<E_F\)), and all states above \(E_F\) are empty (\(f(E)=0 \text{ for } E>E_F\)).

As the temperature increases, thermal excitation generates electron-hole pairs. This leads to an increase in the probability of higher-energy states (\(E>E_F\)) being occupied (because now we have free electrons) and a corresponding decrease in the probability of lower-energy states (\(E<E_F\)) being occupied (because now we have lost electrons from here). In other words, the probability of states being unoccupied—or equivalently, occupied by holes—rises proportionally below \(E_F\). This temperature effect is reflected in the gradual smoothing of the \(f(E)\) curve. Interestingly, most of the changes in occupancy occur near the Fermi level, as shown by the transitions happening in its vicinity.

Note again that at \(E=E_F\), we do not have any electron even though we say chance is 50%. It is just a way of judging how many electrons will there at \(E>=E_c\) by looking at how close or far \(E_F\) is from \(E_c\).

3.3 Thermal-Equilibrium Concentration of Electrons and Holes

The concentration (with respect to energy) of electrons in the conduction band is given by the density of allowed quantum states times the probability that a state is occupied by an electron. This statement is written in equation form as:

\[ n(E) = g_c(E)f(E) \]

where \(n(E)\) is concentration at energy \(E\). The total electron concentration per unit volume in the conduction band is then found by integrating above equation over the entire conduction-band energy.

n_0 = \int g_c(E)f(E) \, dE

Putting in \(g_c(E)\) and \(f(E)\) from above equations and solving the integral results in:

n_0 = N_c\, e^{\dfrac{-(Ec-E_F)}{kT}}

Similarly, holes concentration can be found to be:

p_0 = N_v\,e^{\dfrac{-(E_F-E_v)}{kT}}

where \(N_c\) and \(N_v\) are “effective” density of states and represent total number of states available for occupation in the conduction and valence band, respectively. Remember density of states was function of energy whereas effective density of states is a single value that approximates the total number of available states throughout the energy band.

We see that the thermal-equilibrium concentrations of electrons in the conduction band and of holes in the valence band are directly related to the effective density of states constants and to the Fermi energy level.

3.3.1 The Intrinsic Carrier Concentration

For an intrinsic semiconductor, the concentration of electrons (\(n_i\)) in the conduction band is equal to the concentration of holes (\(p_i\)) in the valence band. Let’s do some math to define \(n_i\) in terms of \(E_g\) and \(T\) which are more familiar terms.

n_i.p_i = N_c\, e^{\dfrac{-(Ec-E_F)}{kT}} \,.\, N_v\,e^{\dfrac{-(E_F-E_v)}{kT}}$$ $$n_i^2 = N_cN_v\, e^{\dfrac{(E_c-E_v)}{kT}}$$ $$n_i^2 = N_cN_v\, e^{\dfrac{-E_g}{kT}}$$ $$n_i = \sqrt{N_cN_v}\, e^{\dfrac{-E_g}{2kT}}

This shows intrinsic carrier concentration is directly related to density of states and exponentially to bandgap and temperature. It also shows that at \(T=0K\), there are no intrinsic carriers that is no free electrons to conduct. This is because electrons are confined to their covalent bonds, there is not thermal energy to break them away.

For Si at T=300K (room temperature), density of free electrons comes out:

n_i\, \text{( @300K T)} = 1.08 \times 10^{10} \; \text{electrons/cm}^3

This may look like a big number but note that Si has \(5\times10^{22}\) atoms/cm³ which means only one in \(5\times10^{12}\) atoms has a free electron at room temperature. Therefore, Si is not of much use in its intrinsic nature! This is why we dope it.

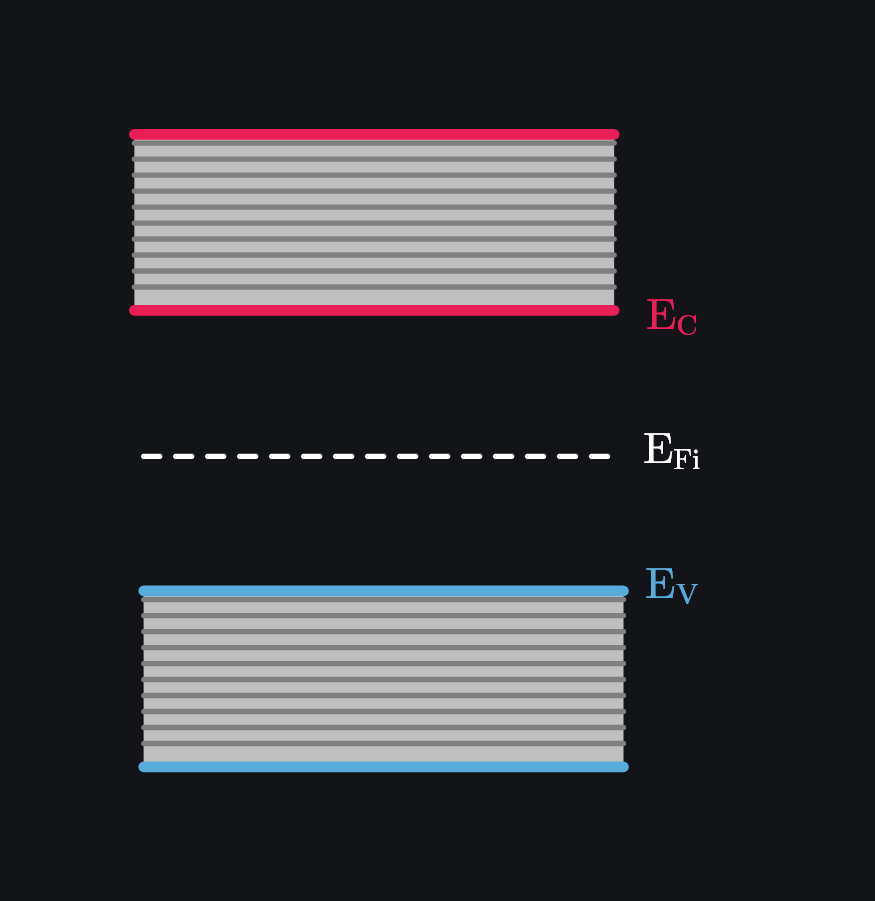
Also note that since intrinsic electrons and holes concentrations are equal, Fermi energy is at midgap as shown in image below. This basically means that if electron occupies, say, 10 states above \(E_F\) somewhere in conduction band, then exact 10 states are also emptied out below \(E_F\) somewhere in valence band (because that is where they came from!). Intrinsic fermi energy is usually represented by \(E_{Fi}\).

3.3.2 Generation and Recombination of Carriers

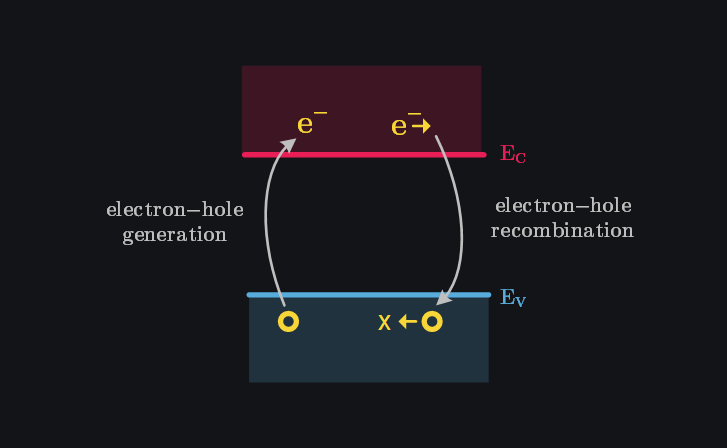
A key nuance in the derivation of intrinsic carrier concentration is that it assumes thermal equilibrium—meaning the carrier concentration remains constant over time. But how does this make sense? We’ve established that electrons are continually being thermally excited from the valence band to the conduction band due to random thermal processes. If this generation kept happening unchecked, electrons would accumulate in the conduction band and holes in the valence band, driving the system out of equilibrium.

So, how is equilibrium maintained? It is through the principle of detailed balance, which states that every process (like generation) is balanced by its reverse process (recombination). Electrons have very high instantaneous thermal velocity, causing them to move randomly through the crystal. During this movement, an electron may pass near an atom missing an electron (a hole) and experience a stronger Coulomb attraction due to the local imbalance of charge. This interaction pulls the electron closer to the atomic nucleus, reducing its potential energy and causing it to transition from the higher-energy conduction band to the lower-energy valence band—effectively “filling” the hole. This process, where the electron annihilates the hole and settles into a more stable configuration, is what we observe as recombination. The energy released during recombination is emitted as light in direct bandgap materials or as heat in indirect bandgap materials, stabilizing the system by moving toward a lower-energy state. Quantum mechanics refines this picture by emphasizing that recombination isn’t a gradual, classical “fall.” Instead, it’s better understood in terms of probability. Due to the inherent uncertainty in an electron’s position, we describe its location with a probability distribution. When the likelihood of finding both an electron and a hole in the same region is high, the electron effectively “snaps” into the hole, completing the recombination process.

For the system to remain in equilibrium, the net carrier concentration must stay constant over time. This requires the rate of generation of electron-hole pairs to be exactly equal to the rate of recombination.

3.5 Doping

To increase the conductivity of Si, we introduce controlled impurities known as dopants, transforming the Si crystal into what’s called an extrinsic semiconductor. For example, adding a group V element like phosphorus, which has five valence electrons, changes the carrier dynamics. Four of these electrons form covalent bonds with neighboring silicon atoms, leaving the fifth electron more loosely bound to the phosphorus atom.

At very low temperatures, this extra electron remains bound to the phosphorus atom. However, it requires significantly less energy to free this electron and promote it to the conduction band compared to the energy needed to excite electrons from silicon’s covalent bonds. Even a small amount of thermal energy is enough to liberate the donor electron, leaving behind a positively charged phosphorus ion.

This process increases the free electron concentration, while the hole concentration decreases because the newly freed electrons tend to recombine with holes present in intrinsic Si. Since electrons now outnumber holes, they are termed majority carriers, while holes become minority carriers. The material is referred to as n-type.

The increase in electron concentration means that the probability of conduction band states being occupied is higher, which causes an upward shift in \(E_F\) closer to the the conduction band. Conversely, in p-type material, \(E_F\) shifts closer to the valence band, indicating a higher occupancy of valence band states. Thus, moving \(E_F\) up or down mathematically encodes the fact that conduction or valence band states are more occupied, respectively.

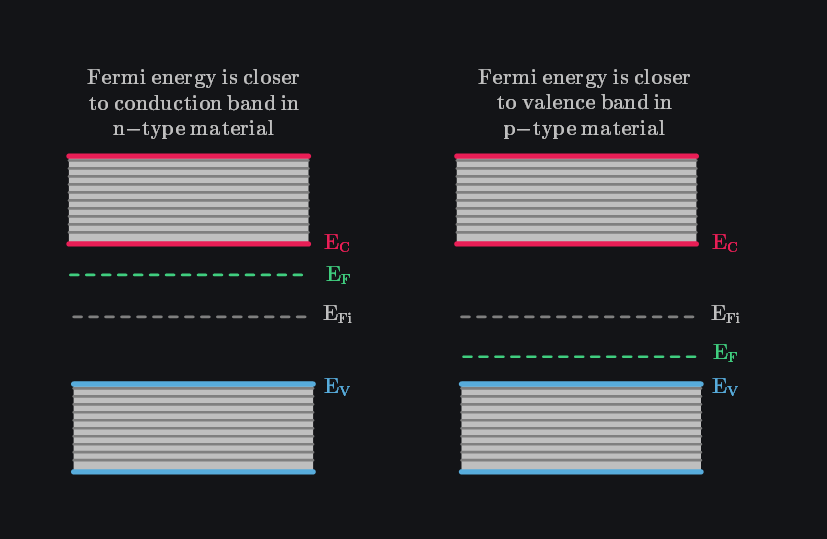
Q: Why Does \(np=n_i^2\) Still Hold?

When we dope a semiconductor, the generation rate of electron-hole pairs remains the same because it depends primarily on the \(E_g\) and \(T\), both of which are unaffected by doping. However, doping increases the recombination rate because more free carriers (either electrons or holes) are available. Increase in n and decrease in p maintains the product \(np\) equals \(n_i^2\). This is one of the fundamental principles of semiconductors in thermal equilibrium. We may think of the intrinsic concentration \(n_i\) simply as a parameter of the semiconductor material.

3.6 Carrier Concentration vs Temperature

We have seen that the intrinsic carrier concentration \(n_i\) is a very strong function of temperature. As the temperature increases, additional electron–hole pairs are thermally generated. At a certain point, the number of thermally generated carriers can exceed the number of electrons contributed by donor atoms, causing the semiconductor to lose its extrinsic properties and become less useful for practical applications.

On the other hand, at low temperatures, donor atoms retain their electrons tightly, preventing them from jumping into the conduction band. In this regime, the donor atoms are only partially ionized, meaning not all of them contribute free electrons. At \(T=0K\), the donor atoms are completely non-ionized, a state known as freeze-out. In this case, the semiconductor again loses its extrinsic characteristics, as the donor atoms no longer provide free carriers.

The image below shows the useful operating range of a silicon semiconductor doped with \(5\times10^{14}\) donor atoms. The optimal temperature range for maintaining the desired extrinsic behavior is approximately \(100–500K\).

Next, let’s go through how charges move inside semiconductor before we finally begin analyzing semiconductor devices.

References

“Semiconductor Physics And Devices: Basic Principles” by Donald A. Neamen

RFInsights

Published: 18 Feb 2023
Last Edit: 18 Feb 2023